Star System Generation in Sine Fine
These past weeks I have been busy working on one of the crucial aspects of the game: the procedural generation of the star system, specifically, the generation of the physical characteristics of the celestial bodies in a specific star system. While the story mode of the game will feature a region of our own galaxy, in the real world we have of course not mapped every system, despite having found several exoplanets. So whenever you will explore a star system, the planets you will find there will have to be procedurally generated, but how?
Methods for Planetary Population Synthesis
“Population synthesis” here being the formal term scientists use to define models of generating star systems and their bodies to test formation theories.
There are several approaches to how this problem could be solved. Maybe you will be familiar with games like Elite Dangerous, whose “Star Forge” has gained some fame as being the underlying system used for procedural generation. No-Man Sky and SpaceEngine being other popular examples. However, implementation details are very scarce.
There are pen-and-paper books that provide rules for the generation of star systems. The most famous one is GURPS: Space. The author recently wrote a new and updated version called Architect of Worlds, which I recommend to anyone favouring a classic dice-based approach.
However, the perfectionist in me would of course want to do it the same way scientists that work on these problems do: with millions of planetesimal-particles and n-body simulations that calculate the results of millions of years of interaction. Essentially, one of the leading theory of planetary accretion as you might know, is the idea that planets forms as a result of merging or accreting smaller planetesimals (bodies of about 100 km in size). Eventually, after millions of years, our Solar system was formed. As we will see in this post, it is not so “simple”.
Side note: after having read several papers in this domain, and coming from another academic albeit in a different field, I really like their work: they run simulations and write papers about it but it’s not for a game, but for science and glory. I digress! Of course, their simulations are much more complicated than what is typically attempted in a game. These two following videos show a rendering software used for this type of n-body simulations on a planetary scales: asteroid collision or the earth and moon colliding (warning: catastrophic space event in the video!).
As my own n-body video above showed, I started toying with an n-body simulator in Unity just because I always wanted to code an n-body algorithm and to see whether such a small-scale “accretion” simulator would be feasible. Of course not. Indeed, it is quickly apparent what the problem might be: a true planetary accretion simulation does not just model the effect of gravity, but several other dynamics at play in a primordial protoplanetary disc, such as the presence of gas drag, heating of the disc, gas dissipation, radiation, and so on.
Even if it was “just” a matter of planting thousands of particles and calling it a day, the space scale would make collisions somewhat rare, without increasing the number of particles by some order of magnitudes. About thirty Earth-sized planets could fit in the distance between the Earth and the Moon. Of course, in million of years these collisions do tend to happen but we haven’t got all day unfortunately. To replicate this approach on a commercial GPU you’d need to be able to simulate hundreds of thousands of particles for quite a long time: the larger the timestep, the higher the possibility of error accumulation.
Accrete by Stephen Dole
Fans of this problem might have heard of this famous paper written by Stephen Dole in 1969. The author defined an algorithm that simulated the accretion process by having planet embryos “sweep” regions of the planetary disc. After each iteration, the protoplanet would accrete “dust” and after having reached a sufficiently large mass, gas as well, leading to the formation of rocky and gas giant planets. Each annulus of the accretion disk would also track the quantity of material left. Potential collisions between protoplanets would also be computed leading to the two bodies merging. This algorithm has been implemented in several languages: here is a js and a c# version.
From the time in which that paper was written (1969) a lot has changed and that algorithm does not consider more recent developments that today we know to be highly likely to be valid models of planetary formation. The two major new theories that have been brought forward are “Pebble accretion” and “Planetary migration”.
Pebble Accretion

The classic “core accretion” theory is that planets form as a result of myriads of collision between “planetesimals”, bodies in the primordial disc of about a 100 km in size (or larger). Even in academic papers, scientists assume so-called “inelastic collisions”, where two bodies collide and form a larger one (to my surprise, not every paper simulates the potential fragmentation resulting from collision impacts). However, this theory alone has been found to have “problems” in explaining how the giant planets in our Solar System were able to form. Protoplanetary discs are formed not just by planetesimals (“dust” or “solids” typically meaning any elements heavier than Hydrogen and Helium, in the astrophysical meaning) but also from gas. The lifetime of gas elements is finite, and many protoplanetary disc tend to dissipate in the range of 1 to 3 million years.
The problem with core accretion is that this process has been shown to require timeframes larger than the lifetime of these protoplanetary discs, which would cause the cores of gas giants to be left with no more gas to accrete after it dissipates. Jupiter is in fact believed to have a rocky core beneath dense layers of gas. Neptune and the other giant planets are smaller than Jupiter by comparison and are seen as “gas giants who didn’t make it”.
To account for this, scientists have proposed the idea that planets might also form via “pebble accretion”. A pebble in this context would be a very small particle of 1 mm to 1 cm that is found in the primordial discs. Once protoplanets reach a sufficient mass, the accretion of these pebbles flowing inward from the outer reaches of the disc becomes much more efficient. Simulations show that this phenomenon can accelerate the formation of planetary rocky cores, enabling gas giants to accrete gas while it is still available.
A potential issue with this model is that it would not explain why the rocky planets in the inner Solar system have such small masses, at least when compared to the giant planets. The idea is that after bodies reach a so-called “Pebble isolation mass”, they effectively block the flow of pebbles further inward. In this way, the flow of these small particles is halted and protoplanets that were created in the inner regions have less pebble material to accrete and must continue to “rely” on the accretion of larger planetesimals.
Planetary Migration

It might turn out that the architecture of our Solar system might not be as common in other systems. You will have heard of hot Jupiters (in your area). It was believed (and is still) that gas giants tended to form farther from the sun, beyond the so-called “snow line”, the distance at which water freezes. With the abundance of other icy materials, it would be “easier” for the cores of these would-be giant planets to find materials, whereas close to a star they would be starved of materials (since icy particles would sublimate the closer to a star they get).
However, exoplanets surveys have revealed quite a few of these hot Jupiters. To explain them, simulations show that the dynamics of the gas present in the accretion disks might lead planets to alter their orbits. This “migration” is typically inward and very slow, in the order of a few AUs per million year and can be of different types depending mainly on the mass of the planet. Even if slow, it could make all the difference if you consider that Jupiter is “currently” at about 5 AUs and moving inward would bring it much closer to our sun (and scatter the inner planets too).
One interesting theory is the so-called Grand Tack where Jupiter might have migrated inward and come as close as 1.5 AU before migrating outwards again to its current position. The Nice model (from Nice in France) also suggests the possibility of migration.
It also means that the migration of planets might cause several consequences. For example, planets might be scattered from their orbits and pushed further inward or even ejected from the system or “accreted” into the sun (i.e. incinerated). It also means that giant planets that have depleted the materials in their vicinity, by migrating they might then come in contact with regions that still have material available.
Putting it all together
After some extensive reading (big thanks to all these papers being available in open-access), I developed the basic “recipe” for the procedural generation system that will be used in Sine Fine. I started from the basics of the system used in Accrete, that is, the representation of an accretion disk as a series of concentric “annuli”. Like in Accrete, each tracks the quantity of dust and gas materials.
Minimum Mass Solar Nebula
At the beginning of the simulation, one such accretion disk is initialised. Different from the original Accrete (which used more empirically determined formulas), I am using actual surface density equations to express the quantity of materials available in each annulus (which is basically a power-law equation based on some assumed dust/gas density parameters). The initial simulation for a 1 M☉ (1 Solar mass) star divides the accretion disk in four regions: 1) the inner zone up to the (early) ice line (0.05-4 au), 2) the “ice zone” (from 4 to 30 AU, current-day location of Neptune); 3) trans-neptunian zone equivalent of the kuiper belt (30 to 60 AU); 4) the outer regions of the solar system (60 to 100 AU). This is because there is a limited “disc mass budget” at the simulation start. For now this is set to 0.015 M☉ for a star like our sun. So if the surface density equations for dust and gas exhaust this “budget”, the amount of material available is made to taper off in these distant annuli.
In papers, this creates the conditions of the so-called MMSN, Minimum Mass Solar Nebula, the minimum specifications that would enable the formation of a system like our own. It is a way to describe the characteristics of a protoplanetary disc, by for example estimating the minimum mass of the materials needed to form the planets of the solar system by considering their current-day mass.
Seeding planetesimals
Successively, a number of planet embryos (for now, a fixed number of 16) are randomly created with masses around 0.1 M🜨 (Eath masses) with increasing orbits (roughly normally distributed around 1.5-2.0 times the previous). If a planet embryo is created in a zone without material, it is removed. Their initial eccentricities and orbit inclination are sampled from a Rayleigh distribution with values coming from papers (in plain words this means that they are in mostly co-planar circular orbits).
Simulation timestep
Every timestep, equivalent to 0.1 Megayears (Myr), Million years, or 100 000 years, the following steps are taken.
- Core Accretion: like in Accrete, each protoplanet sweeps an area around its orbit. This means that the protoplanet can intersect different annuli, which are then split into multiple ones to indicate areas that have been swept and others that still contain material. For a protoplanet in its early stages, this area might be in the range of 0.01 au (it depends on their Hill radius), so if it was located at 1 au that would split the inner annulus that goes from 0.05 to 4 au in three annuli: 0.05 to 0.99 au, 0.99 to 1.01 au, and 1.01 to 4.00 au, of which only that narrow annulus would be depleted of materials (dust).
- Gas Accretion: again, like in Accrete, planets that reach a sufficiently high mass will also accrete gas. This is made on a per-protoplanet basis, since papers seem to indicate that they will accrete as much as gas as it is “provided” by the disc and gas flux.
- Pebble Accretion: differently from Accrete, I have modelled a “pebble flux”, that is a “replenishing” flux of small 1 mm to 1 cm pebbles (independent from the quantity of “dust” in the annuli that are intended to be larger 100 km-sized planetesimal). This pebble flux, according to various papers, can be configured and could be in the order of 100 M🜨/Myr. This represents the quantity of pebbles flowing in from the outer reaches of the disc (or the interstellar medium too, I suppose). Every timestep, some of this material flows in to the outer disc and slowly moves inward. Protoplanets can accrete these pebbles, resulting in a much faster process than with planetesimal accretion alone. Each annulus tracks the quantity of pebbles in its region, independent of the quantity of “dust” planetesimals.
- Planetary Migration:, the two main types of migration are also modelled. Essentially, depending on the protoplanet mass, they will migrate inward at different rates (but in order of a few au/Myr). Planets that get too close to the star will be incinerated (or accreted into the star if you like)!
- Collisions collisions between protoplanets are checked by assuming that if their orbits can cross, then there is a chance they will collide. This is handled purely stochastically (!) “randomly”. A random number is generated, and depending on the outcome the two planetesimal can merge, fragment (resulting in a new protoplanet that has a smaller mass than Ma+Mb, with the leftover material returned to the “Dust” pool), miss each other, or disperse (one of the two is ejected from the system).
- Update: depending on the quantity of materials accreted, the system checks whether protoplanets have reached a mass sufficient to enable gas accretion, or if they have reached “Pebble isolation mass”. This causes the flow of pebbles to stop at the annulus containing that planet, and they won’t be able to flow inward, causing a pebble pile-up. The quantity of gas available is also slowly exponentially depleted, such that after 3 Myr it is mostly gone (but the lifetime can be made dependent on the star characteristics).
- Repeat: after all of this has been done, the simulation continues.
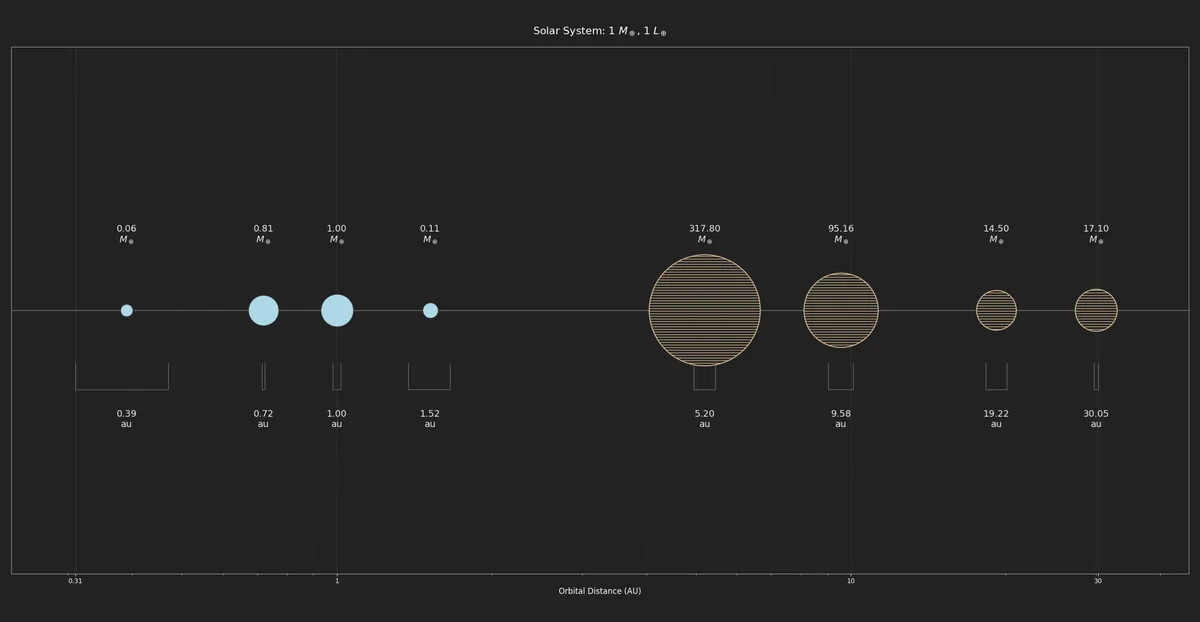
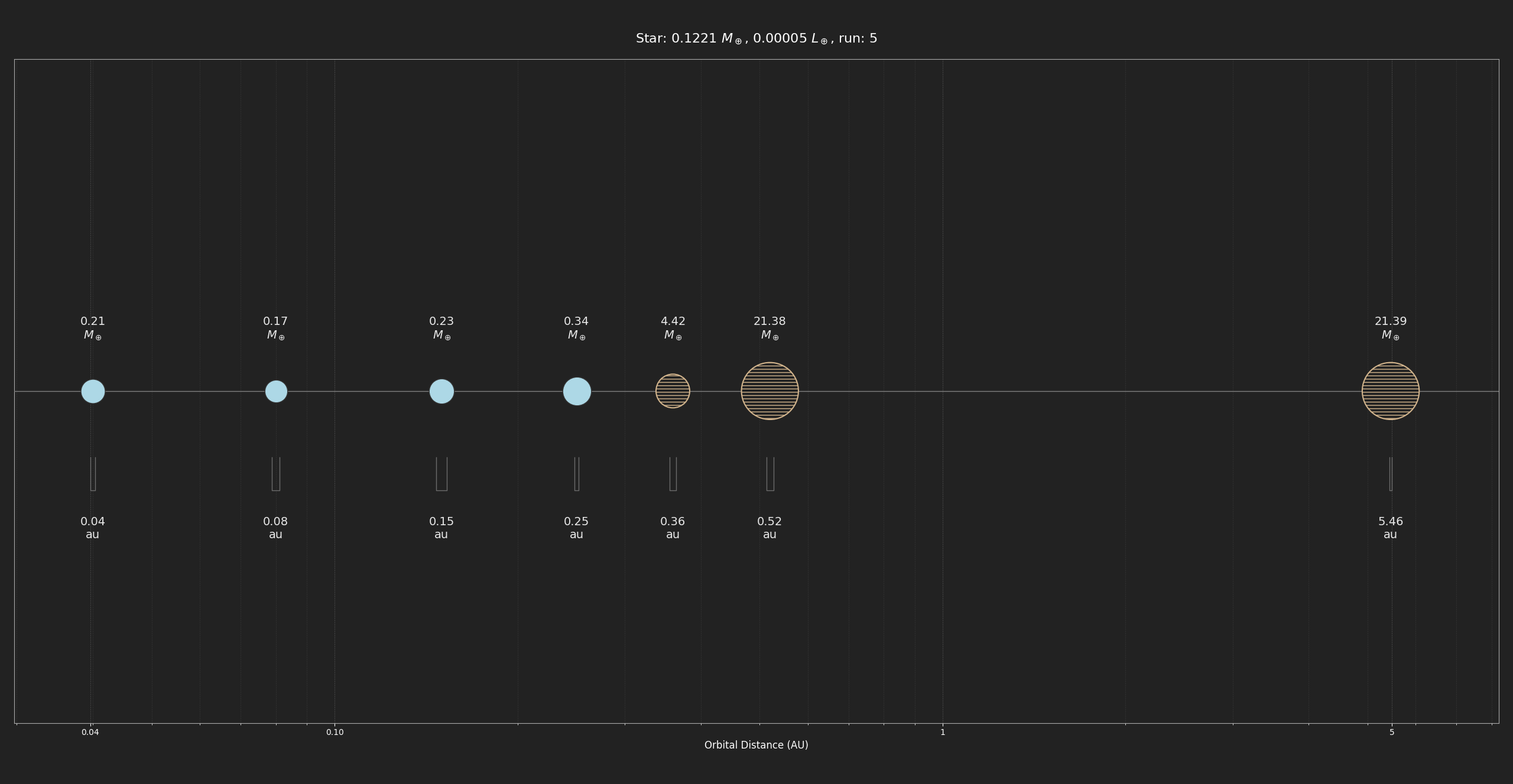
I have run simulations representing 3 Myr (so 300 iterations) on both a star similar to the sun and with a much smaller red dwarf. Results are below. The last picture is our Solar System for reference.





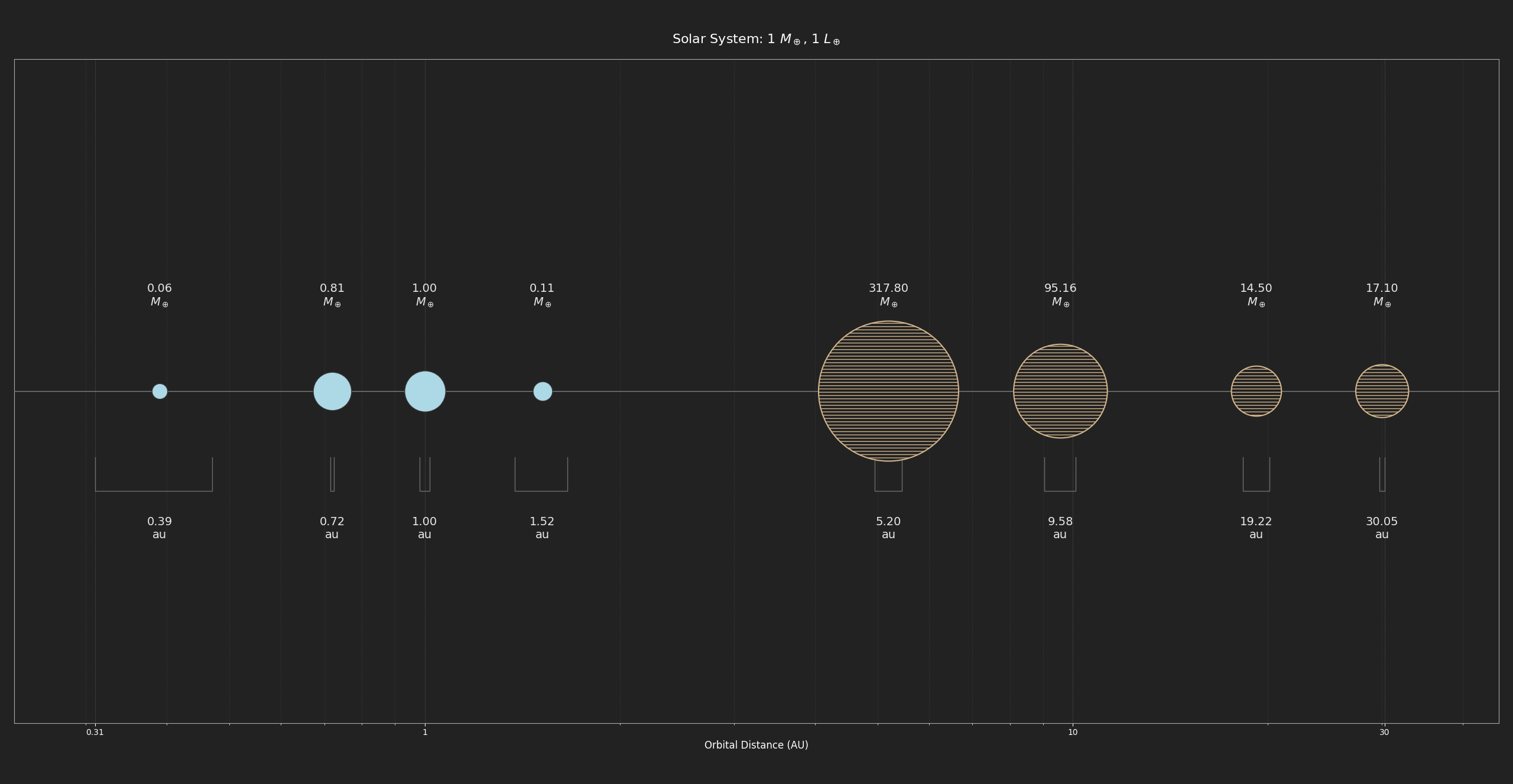
We can see that star systems tend to “correctly” place gas giants further away from the star. Although run 1 and 10 have warm Neptunes (73.75 M🜨 and 43.65 M🜨 at 1.14 and 1.36 au) almost between where Earth and Mars are in our Solar system, a result of planetary migration maybe? There are also some quasi-Jupiters further away. Run 2 has an “interesting” set of three earthlike planets (between 0.7-2.0 M🜨) in a short range of 1.38-1.70 au. Although they look like they overlap in the picture, there are of course millions of km between them. Earthlike candidates? Maybe they could be a bit too cold for our tastes.
In the second set (pictures with 0.1221 M☉) we see that the generated planets are much smaller since there would be less available materials to accrete. In run 5, there seems to be a warm(?) Neptune at 0.52 au of 21.38 M🜨 which is still relatively close for a red dwarf.
Next steps
What the system does not do for now is the “scattering” of planets as giant ones move inward. Protoplanets are also currently generated all at once. To make things more interesting (and to reflect what also happens in academic simulations) would be to have some protoplanets generated at different moments in time. For example, a protoplanet “implanted” later in the life of the disc might not be able to grow to become a Jupiter-like planet because the gas would have dissipated in these later stages.
Then, a planetary “class” needs to be assigned based on the physical characteristics. After all, that’s one of the main goals of the game, to find an earthlike planet!
I also want to add some “flavour” events, such as the capture of random planets that might have different orbital or physical characteristics than the rest of the system (like rogue planets). The beauty of such a system is that some of these naturally arise from the simulation. A “pebble pile-up”? That could become an asteroid belt in-game. A fragmentation event? Suitable conditions for a planetary ring. A near-miss encounter? Maybe if one of the two bodies is much more massive, the smaller one could be captured and become one of its moons.
Limitations
It remains to be seen whether this algorithm tends to generate a wide variety of system. I will need to run the “population synthesis” process hundreds of times and calculate some statistics to have an overview. I am also not entirely sure whether I, as “lay astrophysicist”, am correctly applying the equations (or “prescriptions” as they call them) I have taken from several papers. Probably not!
But abstracting a bit, many of these equations are essentially describing how much mass a planet is accreting or how far it is migrating. These could be replaced by simpler and more linear formulas but in that way we would lose the subtle implications by the various physical characteristics of the protoplanets. For example, some effects tend to increase/decrease depending on the mass or distance of a planet, as it should.
But all in all, I am quite happy with it. It is certainly a good system to build on!
A shorter version of this devlog was also posted on reddit and on the Sine Fine subreddit.